Der Preis der Freiheit ist ewige Wachsamkeit
Thomas Jefferson (1743-1826)

Wozu dienen "numerische Simulationen"?
Viele Vorgänge aus Naturwissenschaft und Technik lassen sich durch mathematische Modelle beschreiben. Beispiele hierfür sind:
- die Vorgänge der Wärme- und Stoffausbreitung (Diffusion)
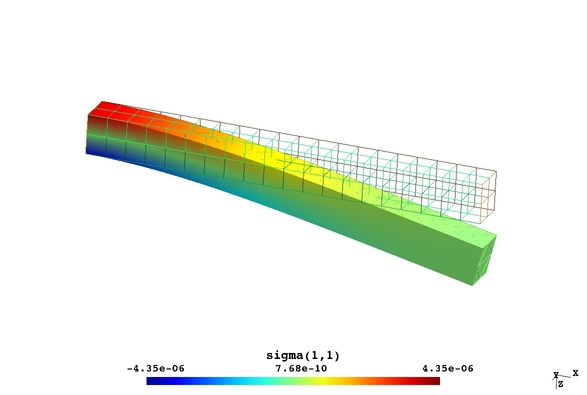
- die Spannungs- und Temperaturfelder in Festkörpern (Festkörpermechanik)
- die Geschwindigkeits-, Spannungs- und Temperaturfelder in Strömungen (Strömungsmechanik)
- die Beschreibung von Wellenausbreitungen (z.B. im Tunnelbau)
- die Regelungsvorgänge eines PID Reglers (z.B. in der Industrie und Gebäudetechnik, SPS)
- die Modelle der künstlichen Intelligenz (AI)
- die Simulation von elektronischen Schaltungen
- die Fast Fourier Transformation (FFT) in der Signalverarbeitung
- die Bewegung von Körpern in der Raumfahrt
Oft lassen sich die mathematischen Modelle mit Hilfe von Differentialgleichungen beschreiben. Diese werden zusammen mit Randbedingungen diskretisiert und numerisch gelöst (numerischen Simulation). Hierfür gibt es eine Reihen von Methoden, z.B. Laplace Transformation, Newton-Verfahren, Gradientenabstiegsverfahren, Finite-Elemente Verfahren (FEM) oder Computational-Fluid-Dynamics (CFD).
Die mathematische Modellbildung sollte dabei dem Prinzip nach Ockham folgen (Ockhams Rasiermesser): das einfachste Modell, welches einen Vorgang beschreibt, ist auch das Wahrscheinlichste.
Mathematisches Modell Differentialgleichungen
+
Randbedingungen | → | Preprocessing / Numerische Berechnung Diskretisierung (Netzerzeugung)
Finite-Elemente Verfahren / Finite-Differenzen Verfahren | → | Postprocessing Graphische Darstellung
der
Simulationsergebnisse |
Die Simulationsergebnisse dienen zur Kostensenkung während des Konstruktionsprozesses, da oft teure Versuche eingespart werden können.
Meine Dienstleistungen:
a) Numerische Berechnungen / Simulationen mit FreeCAD, ElmerFEM, CalculiX und Gmsh
- Simulation von Stoffausbreitung (Diffusion)
- Simulation thermischer Probleme (Wärmeleitung)
- Simulation von Potentialströmungen
- Simulation des Materialverhaltens kundenspezifischer Materialien
b) Data Science
- Auswertung und Visualisierung von Daten mit Hilfe mathematischer Modelle
c) Programmierung / Softwareentwicklung
- Programmierung von Algorithmen mathematischer Modelle
- Technische Client-Server Web-Applicationen
- Softwareentwicklung für Microcontroller
d) Beratung
- in Problemen der Mechanik und Angewandten Mathematik
- in kundenspezifischen Aufgaben der Finite-Elemente Simulation
e) HF Technik